Theorem:
Let a linear time-invariant system ![]() has an
has an
![]() denote the complex sinusoid
denote the complex sinusoid
![]() .
Then,
.
Then,
![]() .
.
Example: Analog RC Lowpass Filter
The impulse response for the circuit in Fig. 1,
i.e. the output measured at ![]() when
when
![]() , is
, is
For a complex sinusoidal input,
![]() ,
,
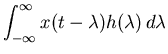 |
|||
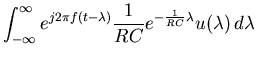 |
|||
![$\displaystyle e^{j2\pi ft} \left[
\frac{1}{RC}\int_{-\infty}^\infty
e^{-j2\pi f\lambda}e^{-\frac{1}{RC}\lambda} d\lambda \right]$](img14.gif) |
|||
![$\displaystyle \left[ \frac{\frac{1}{RC}}{{j2\pi f+\frac{1}{RC}}} \right]
e^{j2\pi ft}$](img15.gif) |
|||
So,
![]() , which is the transfer function of the system.
, which is the transfer function of the system.